24 June 2019

Google CTF 2019

Reverse a Cellular Automata (Reversing)

We have built a cellular automata with 64 bit steps and obeys Wolfram rule 126, it’s boundary condition wraps around so that the last bit is a neighbor of the first bit. Below you can find a special step we chose from the automata.

The flag is encrypted with AES256-CBC, the encryption key is the previous step that generates the given step. Your task is to reverse the given step and find the encryption key.

Flag (Base64): U2FsdGVkX1/andRK+WVfKqJILMVdx/69xjAzW4KUqsjr98GqzFR793lfNHrw1Blc8UZHWOBrRhtLx3SM38R1MpRegLTHgHzf0EAa3oUeWcQ=

Obtained step: 66de3c1bf87fdfcf

We need to calculate the previous step (steps really) that lead to the one given.

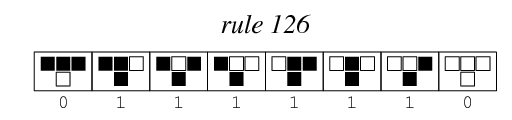
Rule126

For example, the 8bit state 01111001 leads to 11001111, using that rule. But the reverse has more solutions:

When using a 64bit state, as in the instructions to the challenge, the number of possible previous states is quite big. We’ll write a script in z3-solver, to calculate all of them:

Let’s start with the base cell calculation. Given the 3 cells above, return if the cell should be filled or not.

def cell(a,b,c):
    return Or(
        And(a,b,Not(c)),
        And(a,Not(b),c),
        And(a,Not(b),Not(c)),
        And(Not(a),b,c),
        And(Not(a),b,Not(c)),
        And(Not(a),Not(b),c),
    )

Next, the step function for the whole cells in the src state:

def step(src):
    return [ cell( src[i - 1], src[i], src[(i+1) % BITS]) for i in range(BITS)]

The solver:

BITS   = 64
target = 0x66de3c1bf87fdfcf

solver = Solver()

# Define the Bool array that represents the previous state
src = BoolVector("src", BITS)
# Calcula the step
dst = step(src)

# Add constraints to the calculated state, so that it matches our target
for i in range(BITS):    
    mask = 1 << ( BITS - 1 - i)
    solver.add( dst[i] == bool(target & mask) )

We will iterate over all the possible solutions, and print them to generate a dict.

while solver.check() == sat:
    # While it's solvable
    model = solver.model()
    
    # Evaluate the src array, and get all the bits.
    solbits = "".join(['1' if model.eval(src[i]) else '0' for i in (range(BITS))]
    # Print in hex
    print("%x" % int(solbits,2))

    # Add constraing to remove this solution and loop
    solver.add(Or([ model[v]!=v for v in src]))

This is the bash script to run the dictionary:

FLAG64="U2FsdGVkX1/andRK+WVfKqJILMVdx/69xjAzW4KUqsjr98GqzFR793lfNHrw1Blc8UZHWOBrRhtLx3SM38R1MpRegLTHgHzf0EAa3oUeWcQ="
for candidate in `cat dict` ; do
    echo $candidate | xxd -r -p > /tmp/enc.key
    echo $FLAG64 | openssl enc -d -aes-256-cbc -pbkdf2 -md sha1 -base64 --pass file:/tmp/enc.key 2> /dev/null | grep CTF
done

$ python3 solve.py > dict
$ ./brute.sh
CTF{reversing_cellular_automatas_can_be_done_bit_by_bit}

Quantum Key Distribution - Satellite Key Exchange

We are simulating a Quantum satellite that can exchange keys using qubits implementing BB84. You must POST the qubits and basis of measurement to /qkd/qubits and decode our satellite response, you can then derive the shared key and decrypt the flag. Send 512 qubits and basis to generate enough key bits.

Flag: U2FsdGVkX19OI2T2J9zJbjMrmI0YSTS+zJ7fnxu1YcGftgkeyVMMwa+NNMG6fGgjROM/hUvvUxUGhctU8fqH4titwti7HbwNMxFxfIR+lR4=

We need to simulate a Quantum Key Distribution to get the Encryption Key for the flag.

Let’s start by generating 512 quibits, in a base that’s measurable. We need to generate it randomly, or it will get rejected.

# function to generate a random qubit, but measurable in the returned base
def rqubit():
    return random.choice([
        ( { "real": 0.71,  "imag": 0.71}, 'x'), # 1 in x
        ( { "real": -0.71, "imag": 0.71}, 'x'), # 0 in x
        ( { "real": 1.0,   "imag": 0.0 }, '+'), # 0 in +
        ( { "real": 0.0,   "imag": 1.0 }, '+'), # 1 in +
    ])

# Measure a quibit in the specified base. Returns '0' or '1'
def measure(qubit, base):
    if isinstance(qubit, dict):
        qubit = complex(qubit['real'], qubit['imag'])

    if base=="x": 
        qubit *= complex(0.71, -0.71) # Rotate before measurement

    p0 = round(pow(qubit.real, 2), 1)
    p1 = round(pow(qubit.imag, 2), 1)
 
    return str( numpy.random.choice(numpy.arange(0,2), p=[p0,p1]) )    


BITS = 512

qubits_and_basis = [rqubit() for _ in range(BITS)]
qubits, basis = list(zip(*qubits_and_basis))

Once generated, let’s send them to the remote party:


URL = "https://cryptoqkd.web.ctfcompetition.com/qkd/qubits"

post_data = {"basis": basis, "qubits":qubits}

res = requests.post(
    url=URL, 
    json=post_data
)
response = res.json()

We receive two values:

We will select the qubits that were read by the remote party in the same base we generated them.

validbits = ""
for i in range(len(response['basis'])):
    if response['basis'][i] == basis[i]:
        validbits += measure(qubits[i], basis[i])

Finally xor the Distributed Quantum Key, and xor it with the announce (the One Time Pad)

distributedkey = int(validbits[:128],2)
announcement = int(response['announcement'],16)

print("Distributed key: ", hex(distributedkey))
print("Announce (OTP) : ", hex(announcement))
print("Encryption key : ", hex(distributedkey ^ announcement))

$ python3 solve_qkd.py
Distributed key:  `0xdf63b6d25d07bd9eedde2256841c113b`
Announce (OTP) :  `0x4b0f49bec099434eeffd183ce867928a`
Encryption key :  `0x946cff6c9d9efed002233a6a6c7b83b1`

$ FLAG="U2FsdGVkX19OI2T2J9zJbjMrmI0YSTS+zJ7fnxu1YcGftgkeyVMMwa+NNMG6fGgjROM/hUvvUxUGhctU8fqH4titwti7HbwNMxFxfIR+lR4="
$ echo 946cff6c9d9efed002233a6a6c7b83b1 | xxd -r -p > enc.key
$ echo $FLAG | openssl enc -d -aes-256-cbc -pbkdf2 -md sha1 -base64 --pass file:enc.key
CTF{you_performed_a_quantum_key_exchange_with_a_satellite}